Kalman Filters (Tue Nov 19, lect 22) | previous | next | slides |

About Kalman Filters and Sensor Fusion

Viewing: Kalman Filters

Reminder: Readings are your responsibility. You will be expected to come to class prepared, having read the material, and ready to participate in the discussion

Projects

Tip from an article
- For outdoor localizatoin
- QR Code (not feducial) with the true GPS location encoded in the QR code
Project Major Milestone

Kalman Filter?

Kalman “Filter” is a mathematical algorithm
It estimates the true value of an uncertain measurement
Kalman filters are ideal for systems which are continuously changing
Given noisy inputs, for example, GPS, Odom and/or IMU
Calculate, for example, the actual speed of a robot, or the true location of a robot
Makes an “educated guess” about what the system is going to do next.

What question does it try to answer?

Given uncertain sensor data
1. And uncertain state information
2. And uncertain control inputs
3. And uncertain measurements
4. How do you get the best possible estimate of the state?
Well supported by math and statistical analysis
- One key insight two inaccurate readings can be combined into an estimate that is more (not less) accurate than either one alone.
- Assuming errors are truly independent

Learning about Kalman Filters

There is a lot written about it
Because it is difficult and important
The explanations are not consistent and don’t use consistent nomenclature

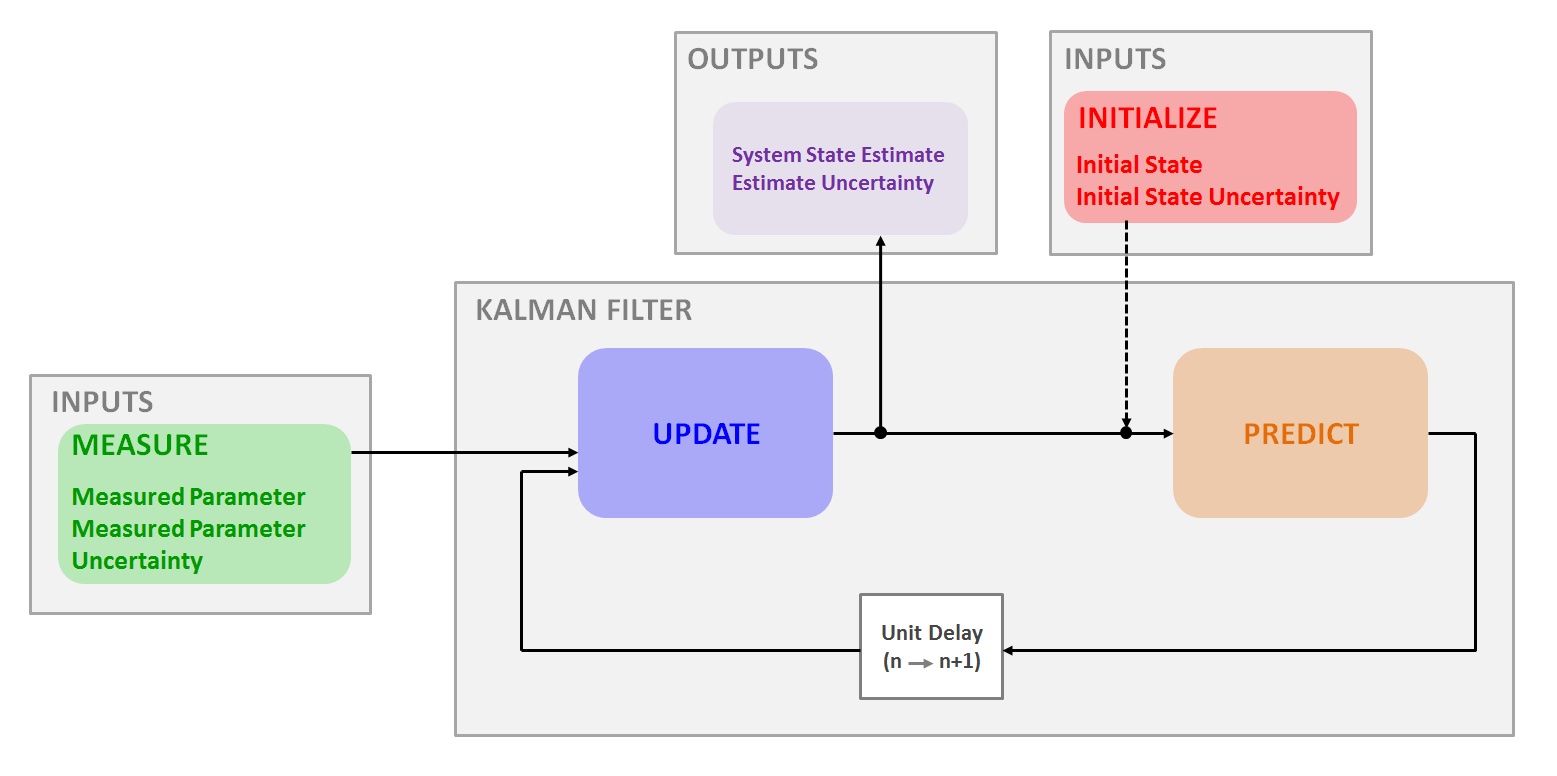
State Estimation

Kalman filter is an iterative model
Each loop tries to make the ESTIMATE of the state more accurate
By processing data from SENSORS (which are statistically characterized)
And considering known control inputs (which are statistically characterized)
And unknown perturbations (which are statistically characterized)
Producing an updated estimate (which is statistically characterized)
The loops happen at intervals that correspond to the rates that sensors are read

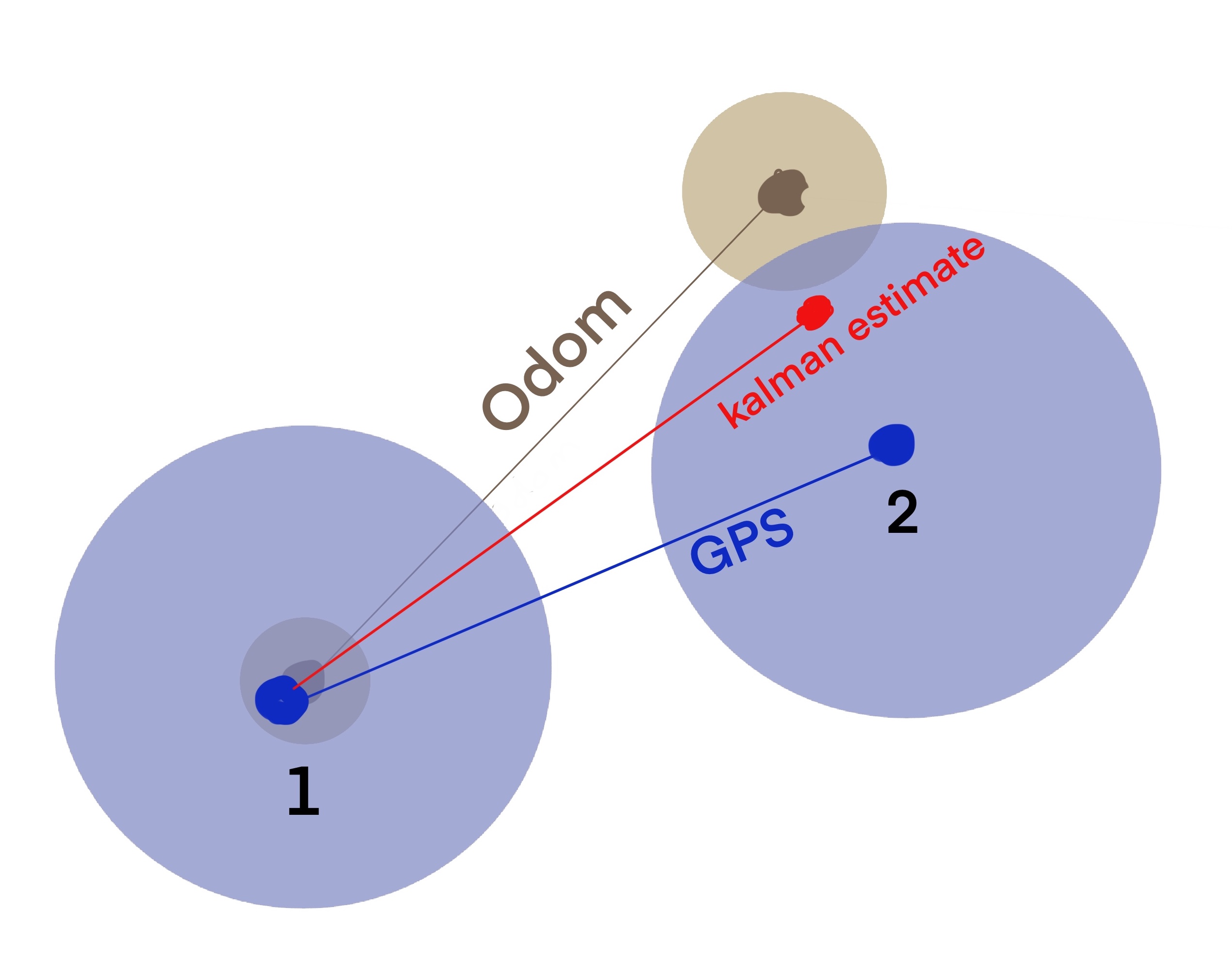
Scenario

An off-road robot moving around a field
Using GPS for localization - which has a known inaccuracy on the order of 5-10 meters
The robot can be asked to move forward or turn at a specified speed or be stationary
State: position and velocity
Control: motion commands
Sensors: GPS … odometry?

Kalman estimate

Why care?

Sensors are everywhere in robotics
Sensors are known to be inaccurate
Kalman filters are a family of algorithms *that give us
More accurate estimates by combining readings with known error rates
They are efficient and they work

System

Kalman filter looks at a “system” which has a “state”
The system state may change over time
1. Based on it’s own internal operation
2. Based on “control” input from the outside
3. Noise or pertrubation
We gain information about the “system”
By sensing data which allow us to infer system changes

Kalman Filter

State model

Based on what is known about the system
We can make a first guess of how the old state would change each step
In other words, if I am at x=0 and I am moving at 1cm / second
Then 1 second later, I am at x=0.01
“all things being equal”
(Note the conceptual similarity to AMCL)

State (X)

a vector (set) of numbers representing the state you are trying to measure (e.g. location)
Vector/Matrix representation is for ease of calculation
But it can also make things look more complicated (for some people)
Usually denoted by X, containing numbers, here are a series of examples
1. current x or y position
2. current speed in the x or y direction
3. current distance from obstacle
4. current altitude from the surface

Covariance Matrix (P)

A way to express the confidence in each component of the state
And the known correlation between them (Σ)

Control Model

Look beyond the internal of the system, what is telling it to change?
Control input:
- Driver steps on break or accelerator
- Gravity is pulling the ball downhill
- cmd_vel is telling the robot to stop
The control model determines the next state given the current state and the control input
Note: The model often has a random component called process noise.

Sensor Model

Given a measurement from the outside world
Important: what is the reliability of the sensor (from spec or empirical measurement)
How does the state model change

1D Scenario: bathroom scale

Using a scale with a known error rate
Sensor generates 10 readings per second
You know that the weight won’t change (ground truth)
What do you use? Average? Moving Average? Or?
What if you have thousands of measurements (10 per second, like a bathroom scale)
Models:
1. State: unchanging (objects weight is not expected to change)
2. Control Inputs: (is an outside agent acting to change) None
3. Measurement Model: (how accurate is the sensor)
4. Update: What is the weight estimate now?
In this situation the Kalman filter does not have an advantage over a simple moving average
Why?

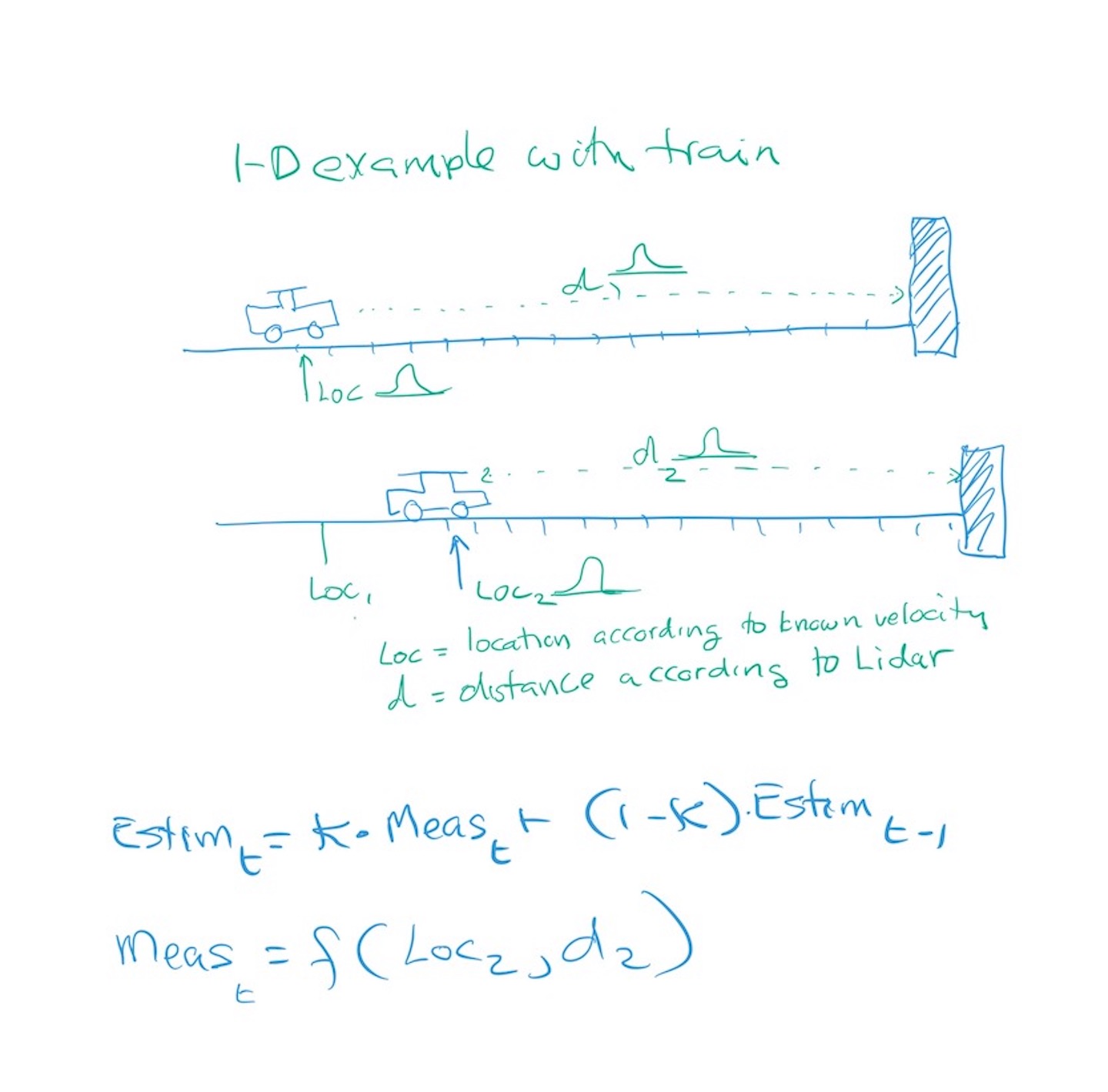
1D Scenario: Train

A train is on a track and moving towards the terminator (which is a block)
Train has a lidar sensing the wall
We have a reading the speed based on the rotation of the wheels
How does the train determine where it is?
Models:
1. State: Location and Velocity. Location changes a known amount each T
2. Control Inputs: (is the driver stepping on the gas): No expected change
3. Measurement model: (How accurate is the Lidar supposed to be)
4. Update: What will be the new location and velocity estimate?

Kalman Train

Abstraction of the Kalman Filter Equations

Diagram of Kalman Filter Equations

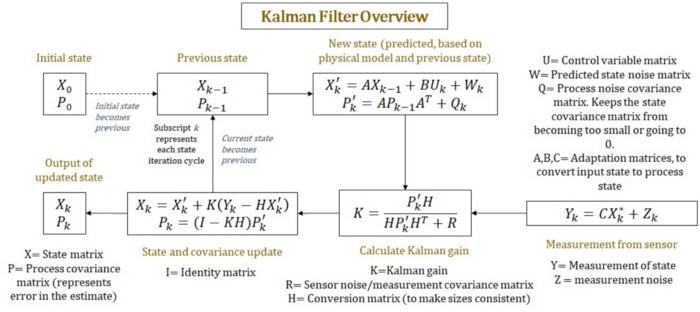
Kalman Gain

Where does the Kalman Gain come from?
There are complex equations which use the covariance matrix with the estimates to compute a Kalman Gain
But I’ve seen examples that skip that and use a constant

How to understand

Most examples you find will use linear algebra (not an expert) and store things in matrices
If the state is location and velocity in the x direction (a falling ball) that is stored in a 1x2 matrix
This simplifies the expression and calculation of the formulas but it is initially confusing
That is unless you are fluent in matrix and linear algebra which I am not

Links for further study